ضرب سه رقمی در یک رقمی: چند ساده ترین روش انجام آن
ضرب اعداد سهرقمی در یکرقمی یکی از مهارتهای پایهای در ریاضیات است که در مقاطع ابتدایی و راهنمایی آموزش داده میشود. این عملیات، اگرچه در نگاه اول ممکن است پیچیده به نظر برسد، با استفاده از روشهای ساده و منظم به راحتی قابل انجام است.
در این مقاله، سه روش ساده و کاربردی برای انجام ضرب اعداد سهرقمی در یکرقمی معرفی میشود. این روشها به گونهای طراحی شدهاند که برای دانشآموزان و افرادی که به دنبال یادگیری سریع و مؤثر هستند، قابل فهم و کاربردی باشند. هدف این است که با زبانی ساده و روان، شما را با این روشها آشنا کنیم تا بتوانید به راحتی این نوع محاسبات را انجام دهید.
روش اول: ضرب به صورت ستونی (روش استاندارد)
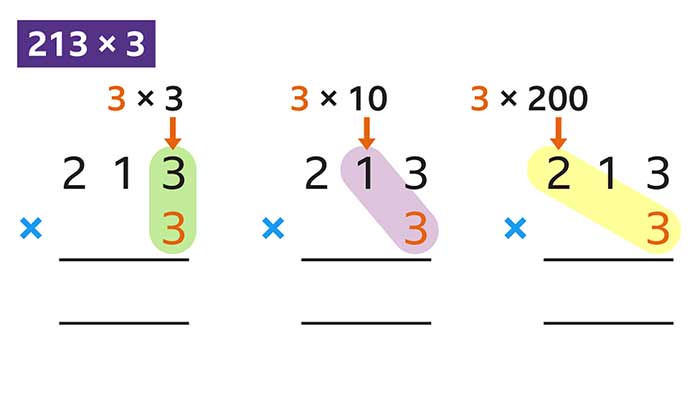
روش ستونی یکی از رایجترین و سادهترین روشها برای ضرب اعداد است که در اکثر کتابهای درسی آموزش داده میشود. این روش به دلیل ساختار منظم و گامبهگام خود، برای همه افراد، بهویژه دانشآموزان، بسیار مناسب است.
مراحل انجام روش ستونی:
- نوشتن اعداد به صورت عمودی: عدد سهرقمی را در بالا و عدد یکرقمی را در پایین بنویسید. به عنوان مثال، فرض کنید میخواهیم ۴۵۶ را در ۷ ضرب کنیم:
۴۵۶× ۷
- ضرب هر رقم به صورت جداگانه: از سمت راست (رقم یکان) شروع کنید. ابتدا رقم یکان عدد سهرقمی (۶) را در ۷ ضرب کنید: ۶ × ۷ = ۴۲. عدد ۲ را در زیر خط بنویسید و ۴ را به عنوان «انتقال» به ستون بعدی یادداشت کنید.
- ضرب رقم دهگان: رقم دهگان (۵) را در ۷ ضرب کنید: ۵ × ۷ = ۳۵. حالا ۴ (انتقال از مرحله قبل) را به آن اضافه کنید: ۳۵ + ۴ = ۳۹. عدد ۹ را بنویسید و ۳ را به ستون بعدی منتقل کنید.
- ضرب رقم صدگان: رقم صدگان (۴) را در ۷ ضرب کنید: ۴ × ۷ = ۲۸. سپس ۳ (انتقال) را اضافه کنید: ۲۸ + ۳ = ۳۱. عدد ۳۱ را بنویسید.
- نتیجه نهایی: با کنار هم قرار دادن اعداد، نتیجه ۳۱۹۲ خواهد بود.
- ۴۵۶× ۷=۳۱۹۲
مزایای روش ستونی:
- ساختار منظم و قابل فهم.
- مناسب برای اعداد بزرگتر.
- کاهش احتمال خطا با تمرین.
روش دوم: تجزیه عدد سهرقمی
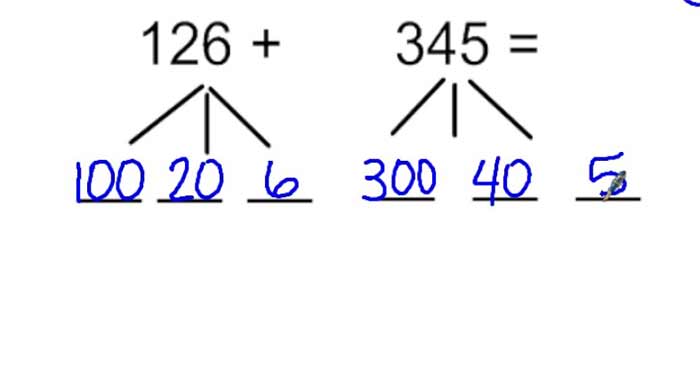
روش تجزیه به شما امکان میدهد عدد سهرقمی را به اجزای کوچکتر تقسیم کنید و هر بخش را جداگانه ضرب کنید. این روش برای افرادی که با اعداد کوچکتر راحتتر هستند، بسیار کاربردی است.
مراحل انجام روش تجزیه:
- تجزیه عدد سهرقمی: عدد سهرقمی را به صدگان، دهگان و یکان تقسیم کنید. برای مثال، ۴۵۶ را میتوان به صورت ۴۰۰ + ۵۰ + ۶ نوشت.
- ضرب هر بخش: هر بخش را به صورت جداگانه در عدد یکرقمی ضرب کنید:
- ۴۰۰ × ۷ = ۲۸۰۰
- ۵۰ × ۷ = ۳۵۰
- ۶ × ۷ = ۴۲
- جمع نتایج: نتایج بهدستآمده را با هم جمع کنید:
۲۸۰۰ + ۳۵۰ + ۴۲ = ۳۱۹۲
مزایای روش تجزیه:
- سادهسازی محاسبات با تقسیم عدد به بخشهای کوچکتر.
- مناسب برای یادگیری مفهومی ضرب.
- کمک به درک بهتر ارزش مکانی اعداد.
روش سوم: ضرب ذهنی با سادهسازی
این روش برای افرادی مناسب است که میخواهند ضرب را به صورت ذهنی و سریع انجام دهند. در این روش، از ویژگیهای خاص عدد یکرقمی برای سادهسازی محاسبات استفاده میشود.
مراحل انجام روش ذهنی:
- انتخاب یک عدد نزدیک: اگر عدد یکرقمی نزدیک به ۱۰ باشد (مثل ۹ یا ۸)، میتوانید از تکنیکهای سادهسازی استفاده کنید. برای مثال، برای ضرب ۴۵۶ × ۹:
- ابتدا ۴۵۶ را در ۱۰ ضرب کنید (۴۵۶ × ۱۰ = ۴۵۶۰)، زیرا ضرب در ۱۰ ساده است.
- سپس ۴۵۶ را از نتیجه کم کنید، چون ۹ = ۱۰ – ۱:
۴۵۶۰ – ۴۵۶ = ۴۱۰۴
- بررسی نتیجه: برای اطمینان، میتوانید از روش ستونی یا تجزیه استفاده کنید تا نتیجه را تأیید کنید.
مزایای روش ذهنی:
- سرعت بالا در محاسبات.
- مناسب برای تمرین ذهنی و تقویت مهارتهای ریاضی.
- کاربردی برای اعداد یکرقمی خاص (مثل ۵، ۹ یا ۱۰).
نکات مهم برای بهبود مهارت ضرب
- تمرین منظم: هرچه بیشتر تمرین کنید، سرعت و دقت شما در انجام ضرب افزایش مییابد.
- استفاده از ابزارهای بصری: جدول ضرب یا ماشینحساب (برای بررسی نتایج) میتواند به یادگیری کمک کند.
- تقسیم مسئله به بخشهای کوچکتر: اگر محاسبات پیچیده به نظر میرسند، همیشه میتوانید از روش تجزیه استفاده کنید.
- بررسی خطاها: پس از انجام محاسبه، نتیجه را با روش دیگری بررسی کنید تا از صحت آن مطمئن شوید.
کدام روش بهتر است؟
انتخاب روش مناسب به نیازها و مهارتهای شما بستگی دارد. اگر به دنبال دقت و ساختار هستید، روش ستونی بهترین گزینه است. اگر میخواهید مفهوم ضرب را بهتر درک کنید، روش تجزیه مناسبتر است. برای محاسبات سریع و ذهنی، روش سوم ایدهآل است. بهتر است هر سه روش را تمرین کنید تا در موقعیتهای مختلف بتوانید از آنها استفاده کنید.
مثالهای بیشتر
برای تثبیت یادگیری، چند مثال دیگر را بررسی میکنیم:
- مثال ۱: ۳۲۳ × ۴
- روش ستونی: ۳۲۳ × ۴ = ۱۲۹۲
- روش تجزیه: (۳۰۰ × ۴) + (۲۰ × ۴) + (۳ × ۴) = ۱۲۰۰ + ۸۰ + ۱۲ = ۱۲۹۲
- مثال ۲: ۵۴۸ × ۶
- روش ستونی: ۵۴۸ × ۶ = ۳۲۸۸
- روش ذهنی (برای ۶): ابتدا ۵۴۸ × ۵ = ۲۷۴۰، سپس ۵۴۸ را اضافه کنید: ۲۷۴۰ + ۵۴۸ = ۳۲۸۸
ترفندهای جدیدتر
| نام ترفند | توضیح ترفند | مراحل انجام | مثال (۴۵۶ × ۷) | مزایا |
| ترفند دو نیمه | عدد سهرقمی را به دو بخش تقسیم کنید (دو رقم اول و رقم آخر) و هر بخش را جداگانه ضرب کنید، سپس نتایج را با تنظیم مناسب جمع کنید. | ۱. عدد سهرقمی را به دو بخش تقسیم کنید: دو رقم اول (دهگان و صدگان) و رقم یکان. ۲. بخش اول را در عدد یکرقمی ضرب کنید. ۳. بخش دوم (یکان) را در عدد یکرقمی ضرب کنید. ۴. نتایج را با توجه به ارزش مکانی (اضافه کردن یک صفر به بخش اول) جمع کنید. | ۴۵۶ را به ۴۵ و ۶ تقسیم کنید. ۱. ۴۵ × ۷ = ۳۱۵ ۲. ۶ × ۷ = ۴۲ ۳. به ۳۱۵ یک صفر اضافه کنید (۳۱۵۰) و با ۴۲ جمع کنید: ۳۱۵۰ + ۴۲ = ۳۱۹۲ | – سادهسازی با تقسیم به دو بخش. – مناسب برای محاسبات ذهنی سریع. – درک آسان ارزش مکانی. |
| ترفند معکوس | از عدد یکرقمی برای سادهسازی استفاده کنید و ضرب را از چپ به راست انجام دهید، با انتقالهای معکوس. | ۱. از رقم صدگان شروع کنید و آن را در عدد یکرقمی ضرب کنید. ۲. نتیجه را ۱۰۰ برابر کنید (دو صفر اضافه کنید). ۳. رقم دهگان را ضرب کنید، یک صفر اضافه کنید و به نتیجه قبلی اضافه کنید. ۴. رقم یکان را ضرب کرده و به نتیجه اضافه کنید. | ۱. ۴ × ۷ = ۲۸، پس ۲۸۰۰ (دو صفر). ۲. ۵ × ۷ = ۳۵، پس ۳۵۰ (یک صفر). ۳. ۲۸۰۰ + ۳۵۰ = ۳۱۵۰. ۴. ۶ × ۷ = ۴۲، پس ۳۱۵۰ + ۴۲ = ۳۱۹۲. | – مناسب برای محاسبات از چپ به راست. – کاهش نیاز به انتقالهای پیچیده. – جذاب برای تمرین ذهنی. |
| ترفند ضریب مقیاس | عدد سهرقمی را با یک ضریب مقیاس (مثل ۱۰ یا ۵) ساده کنید و سپس نتیجه را تنظیم کنید. | ۱. عدد یکرقمی را به یک عدد ساده (مثل ۱۰) نزدیک کنید. ۲. عدد سهرقمی را در این عدد ساده ضرب کنید. ۳. اختلاف بین عدد ساده و عدد اصلی را محاسبه کنید. ۴. نتیجه را با توجه به اختلاف تنظیم کنید. | برای ۴۵۶ × ۷: ۱. ۷ را به ۱۰ نزدیک کنید (۷ = ۱۰ – ۳). ۲. ۴۵۶ × ۱۰ = ۴۵۶۰. ۳. اختلاف: ۴۵۶ × ۳ = ۱۳۶۸. ۴. ۴۵۶۰ – ۱۳۶۸ = ۳۱۹۲. | – سرعت بالا با استفاده از اعداد ساده. – مناسب برای اعداد نزدیک به ۵ یا ۱۰. – تقویت مهارتهای ذهنی. |
- ترفند دو نیمه: این روش عدد سهرقمی را به دو بخش کوچکتر تقسیم میکند و محاسبات را سادهتر میکند، بهویژه برای کسانی که با اعداد دورقمی راحتتر هستند.
- ترفند معکوس: این روش برعکس روش ستونی عمل میکند و برای افرادی که ترجیح میدهند از چپ به راست محاسبه کنند، جذاب است.
- ترفند ضریب مقیاس: این روش از اعداد کلیدی مثل ۱۰ استفاده میکند تا محاسبات سریعتر شوند و برای اعداد یکرقمی خاص (مثل ۷ یا ۸) بسیار مؤثر است.
این ترفندها به گونهای طراحی شدهاند که هم جدید باشند و هم به شما کمک کنند تا با روشهای متنوع، مهارت ضرب خود را تقویت کنید. برای تمرین، هر ترفند را با اعداد مختلف امتحان کنید تا ببینید کدامیک برای شما مناسبتر است.
نتیجهگیری
ضرب اعداد سهرقمی در یکرقمی نیازی به پیچیدگی ندارد. با استفاده از روشهای ستونی، تجزیه یا ذهنی، میتوانید این محاسبات را به راحتی انجام دهید. هر روش مزایای خاص خود را دارد و با تمرین، میتوانید در هر یک از آنها مهارت پیدا کنید. پیشنهاد میشود ابتدا با روش ستونی شروع کنید و سپس روشهای دیگر را امتحان کنید تا ببینید کدامیک برای شما راحتتر است. این مهارت نهتنها در ریاضیات школьیدر زندگی روزمره نیز به کار میآید.




